Codeforces Round #551 (Div.2) A~D
매주 코드포스 버추얼을 도는 스터디를 하는데, 최근 라운드들은 다른 스터디원들이 이미 풀어본 라운드가 많아서 오래전 라운드부터 진행하고 있다. 재작년 라운드까지 거슬러올라가서 진행했고 그 풀이를 여기 적는다.
A. Serval and Bus

비가 오는데 Serval은 버스를 타야 한다고 한다. 그래서 Serval이 버스 정류장에 도착하는 시간이 주어지고, 각 버스가 정류장에 처음 도착하는 시간과 배차간격이 주어진다. 버스 정류장에 도착하는 시간을 포함하여 그 뒤 시간에 가장 빨리 오는 버스를 타고 Serval은 떠난다. 이때 Serval이 타는 버스가 몇 번째 버스인지 찾으면 되는 문제이다.
물론 배차간격으로 나누고 어쩌고 해가면서 수학적으로 풀 수도 있겠지만, 하나씩 다 해봐도 된다. 버스 노선은 최대 100개밖에 안 되고 기다리는 시간도 10만 제한밖에 안 된다. 따라서 모든 버스노선에 대해, 버스가 정류장에 도착하는 시간 중 Serval이 도착하는 시간과 가장 가까운 것을 하나하나 찾아서, Serval이 기다리는 시간을 계산하고 나서 그 기다리는 시간이 가장 작은 버스노선을 찾으면 된다. 넉넉하게 대충 생각해도 1000만의 연산횟수. 시간 내에 충분히 돈다.
#include <iostream>
#include <vector>
#include <list>
#include <cstring>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <cmath>
typedef long long ll;
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n, t;
cin >> n >> t;
int wait[105] = { 0 };
for (int i = 1; i <= n; i++) {
int s, d;
cin >> s >> d;
wait[i] = s;
while (s < t) {
s += d;
}
wait[i] = s - t;
}
int ans = 0, w = 1000000;
for (int i = 1; i <= n; i++) {
if (w > wait[i]) { w = wait[i]; ans = i; }
}
cout << ans << "\n";
return 0;
}
B. Serval and Toy Bricks

정육면체 블럭을 쌓아서 만든 어떤 입체를 앞에서 본 모양, 옆에서 본 모양, 위에서 본 모양이 주어진다. 그것을 보고 원래의 입체가 어떻게 구성되어 있는지를 재구성하면 되는 문제다. 가능한 모양이 많으면 모두 출력해 준다.
위에서 본 모양을 통해 어느위치에 블럭이 쌓여 있는지를 알 수 있다. 이때 블럭이 쌓여 있지 않은 곳은 신경쓸 필요가 없다. 블럭이 쌓여 있는 위치의 경우 앞에서 본 모양/옆에서 본 모양을 통해 블럭의 개수를 유추할 수 있다. 이때 앞에서 본 모양은 그 열에서 가장 높은 높이의 블럭, 옆에서 본 모양은 그 행에서 가장 높은 높이의 블럭이므로, 칸마다 둘 중 작은 것을 택해서 배치하면 된다. 코드를 보는 게 이해가 빠르다.
#include <iostream>
#include <vector>
#include <list>
#include <cstring>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <cmath>
typedef long long ll;
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n, m, h;
cin >> n >> m >> h;
int matrix[105][105];
int front[105], side[105];
for (int i = 0; i < m; i++) {
cin >> front[i];
}
for (int i = 0; i < n; i++) {
cin >> side[i];
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> matrix[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (matrix[i][j]) {
matrix[i][j] = min(side[i], front[j]);
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cout << matrix[i][j] << " ";
}
cout << "\n";
}
return 0;
}
C. Serval and Parenthesis Sequence

'짝이 맞는 괄호'에 관한 엄청나게 많은 문제들 중 하나다. '('과 ')' 그리고 '?'로 이루어진 문자열이 주어진다. 이때 ?들을 '('과 ')' 중 하나로 바꿔서 짝이 맞는 괄호 문자열로 만드는 것이 과제이다. 단 조건이 있는데, 만들어진 괄호 문자열의 prefix들 중 짝이 맞는 괄호 문자열이 존재하면 안 된다. 가령 ()() 같은 문자열은 짝이 맞는 문자열이지만 prefix중 '()'가 짝이 맞는 괄호 문자열이므로 조건에 맞지 않는다. (()) 같은 건 조건을 충족한다. 짝이 맞는 괄호 문자열이지만, 그 어떤prefix 문자열도 짝이 맞지 않는다.
먼저, 조건에 맞게 문자열을 변경하는 게 불가능한 경우부터 생각해 보자.
- 문자열의 길이가 홀수일 경우 당연히 짝이 맞는 문자열을 만들 수 없다.
- ?를 제외하고, 기존에 있는 '('의 개수나 ')'의 개수가 문자열의 길이의 반을 넘을 경우 '?'들을 가지고 무슨 짓을 해도 짝을 맞출 수 없다.
그 두 가지를 먼저 제외하고 나면 '?'들에 괄호를 채워넣는 일만 남았다. 궁극적으로는 여는 괄호와 닫는 괄호 둘 다 n/2개가 있어야 하므로(n은 문자열의 길이) 그걸 채워넣는 작업을 진행한다. 이때 prefix들이 짝이 맞는 걸 방지하기 위해 '('부터 모두 채우고 나서 ')'를 채운다. 만약 어떤 이유로든 이를 다 채울 수 없으면 짝이 맞는 괄호문자열을 만들 수 없다.
그렇게 괄호 문자열을 다 체크하고 나면 마지막으로, prefix들 중 짝이 맞아버린 괄호 문자열이 없는지 체크한 후, 만든 문자열을 출력해 주면 된다.
#include <iostream>
#include <vector>
#include <list>
#include <cstring>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <cmath>
typedef long long ll;
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int len;
string s;
cin >> len >> s;
if (len % 2 == 1) { cout << ":(\n"; }
else {
int open = 0, close = 0;
for (int i = 0; i < len; i++) {
if (s[i] == '(') { open++; }
else if (s[i] == ')') { close++; }
}
if (open > len / 2 || close > len / 2) { cout << ":(\n"; return 0; }
//마지막에는 여는 괄호 닫는 괄호 각각 len/2개씩 있어야
open = len / 2 - open; close = len / 2 - close; //이만큼씩 채워져야함
int cnt = 0;
for (int i = 0; i < len; i++) {
if (s[i] == '?') {
if (open) {
open--;
s[i] = '(';
}
else {
close--;
s[i] = ')';
}
}
}
if (open || close) { cout << ":(\n"; }
else {
open = 0; close = 0;
for (int i = 0; i < len; i++) {
//마지막 체크
if (s[i] == '(') { open++; }
else { close++; }
if (close > open || (open == close && i < len - 1)) { cout << ":(\n"; return 0; }
}
}
cout << s << "\n";
}
return 0;
}
D. Serval and Rooted Tree

내가 정말 못하는 재귀가 나와서 정말 개빡셌다. 시간 내에 못 푼 건 물론이고 재귀 없이 푸는 방법을 찾기 위해 온갖 짓을 다 하고 남의 코드도 수십 개는 보고 며칠 동안 개삽질을 했는데 아무 소득도 없었다. 그냥 내가 재귀를 익히는 게 빠를 것 같아서 재귀 코드를 이해하여 올린다.
문제 설명을 하자면, 어떤 트리가 주어진다. 그리고 그 리프 노드들의 숫자가 k라고 하면, 리프노드들에 1부터 k까지의 숫자를 붙여야 한다. 이때 트리의 모든 노드들에는 'max'혹은 'min'이라는 라벨이 붙어 있는데, 'max'라벨이 붙은 노드의 경우 그 노드는 자식들 중 가장 큰 값을 갖는 노드의 값을 똑같이 가진다. 'min'라벨이 붙은 노드의 경우에는 자식들 중 가장 작은 값을 갖는 노드의 값을 똑같이 가진다. 각 노드들에 어떤 라벨이 붙어 있는지가 주어지고 우리는 트리의 루트 노드가 갖는 값이 최대가 되도록, 리프 노드들에 숫자를 배치해야 한다. 그때의 루트 노드가 갖는 값을 구하면 된다.
먼저 간단한 트리를 생각해 보자. (트리의 일부일 수 있는 예시 그림일 뿐이고, 그림의 루트노드에도 사실 부모가 있을 수 있고 그림의 리프노드에도 자식들이 있을 수 있다. 적절히 이해해야 한다)
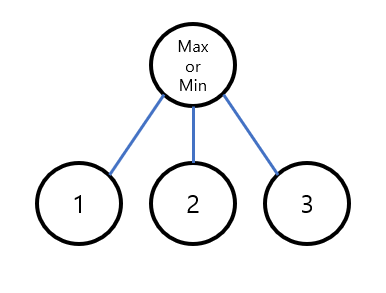
위와 같은 구조의 트리에서, 만약 루트에 max라벨이 붙어 있다면 루트노드 값은 3일 것이고, 루트에 min라벨이 붙어 있다면 루트 노드 값은 1일 것이다. 그런데 만약 위의 그림과 같은 노드를 dfs 중에 만났다고 해보자. 만약 노드의 라벨이 max이면 3으로 최댓값이 보존된다. 그러나 노드의 라벨이 min이면 노드에 1이 저장되므로 2만큼을 잃었다(이2는 엄밀히 말하면 숫자 2가 아니라, 노드의 자식들에 숫자들을 최적으로 배치했을 때 최솟값 노드를 제외한 나머지 노드들의 개수이다)
리프노드에서 올라가는 것으로 생각해도 된다. 리프노드들이 루트를 향해 올라가다가 max라벨 노드를 만날 경우에는 리프노드들의 최댓값이 보존된다. 그러나 위로 올라가면서 min라벨 노드를 만날 경우, 그 노드 밑에 있는 자식들의 최솟값을 취하게 되므로, 반대로 생각하면 '기존의 최댓값'에서 'min라벨 노드의 서브트리에서 잃어버린 노드들의 수만큼' 을 잃는다고 생각할 수 있다. 숫자가 최적으로 배치되어 있다고 가정하기에 이런 생각이 가능하다.
이런 생각을 그대로 코드로 옮길 시, max라벨 노드의 경우 그냥 넘어가고, min라벨 노드의 경우 (그 서브트리 사이즈-1)만큼을 잃어버린다고 생각하면서 dfs를 하는 코드를 짤 수 있다. 마지막으로 그 잃어버린 노드의 개수를 리프노드 개수에서 빼주면 그게 정답이다. 최소한으로 값을 잃어버리면서 리프노드에서 시작해 루트노드에 도달한 값이므로 그 값이 루트노드의 최댓값이다. 솔직히 아직도 좀 알쏭달쏭해서 실력을 키워야 함을 느낀다.
#include <iostream>
#include <vector>
#include <list>
#include <cstring>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <cmath>
#include <queue>
typedef long long ll;
using namespace std;
int leaf, maxmin[300005], parent[300005];
vector<int> adj[300000];
int dfs(int pos) { //'잃어버리는' 리프 노드들의 개수를 계산한다
if (adj[pos].empty()) { return 0; } //자식이 없으면 잃을 것도 없다
if (maxmin[pos]) { //max쿼리의 경우
int res = 300005;
for (int next : adj[pos]) {
res = min(res, dfs(next));
}
return res;
}
else {
int res = 0;
for (int next : adj[pos]) {
res += dfs(next);
}
return res + adj[pos].size() - 1;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> maxmin[i];
}
for (int i = 1; i < n; i++) {
cin >> parent[i]; //0이 root
parent[i]--;
adj[parent[i]].push_back(i); //부모노드에 자식 연결
}
for (int i = 0; i < n; i++) {
if (adj[i].empty()) {
maxmin[i] = 1; leaf++; //리프노드는 max쿼리인걸로 처리해도 됨. 그리고 리프노드 숫자를 세준다
}
}
cout << leaf - dfs(0) << "\n";
return 0;
}

