Heavy Light Decomposition
다음과 같은 문제를 생각해보자.
크기가 N인 배열에서 주어지는 [l,r] 범위들의 합을 각각 구하여라.
이 글을 찾아올 정도의 사람이라면 아마 일일이 더하는 것이 아니라 누적합을 구해서 각 쿼리를 O(1)에 처리할 것이다.
저 배열에 단일점 업데이트가 있다면 세그먼트 트리를 쓸 것이고, 구간 업데이트가 있다면 Lazy propagation을 얹어서 쓸 것이고.. 뭐 암튼 선형 자료구조라면 대부분의 문제를 세그먼트 트리를 가지고 비벼볼 수 있다.
선형구조인 배열이 아닌 트리에서는 어떻게 해야할까?
배열이 트리로 바뀌고 트리의 각 정점에 어떤 값이 저장되어있다고 한다면 위의 문제는 다음과 같이 바뀔 것이다.
크기가 N인 트리에서 주어지는 [u,v] 경로들에 포함된 정점들의 가중치의 합을 각각 구하여라.
가장 나이브한 방법은 u에서 v까지 일일이 탐색하면서 만나는 점들의 값을 하나씩 더해주는 것이다. 시간복잡도는 당연하게도 쿼리당 O(N). O(logN)이라고 생각했다면 일자로 쭉 펴진 트리를 생각해보자.
모범적인 답은 배열에서 누적합을 저장해두듯이 트리에서 각 정점에서 2k에 해당하는 부모정점과 거기까지의 누적합을 미리 계산해서 각 쿼리마다 O(logN) 정도에 처리를 하는 것이다.
하지만 이 방법도 정점에 업데이트가 있다면 사용할 수 없다. 세그먼트 트리를 박을 수 있다면 참 좋겠지만 아쉽게도 정점들이 연속적이지 않아 써먹을 수가 없다. 그렇다면 트리를 잘 쪼개서 선형인 구조가 여러 개 존재하는 형태로 만들면 되지 않을까?
예를 들어 아래의 그림과 같은 트리가 존재한다고 하면
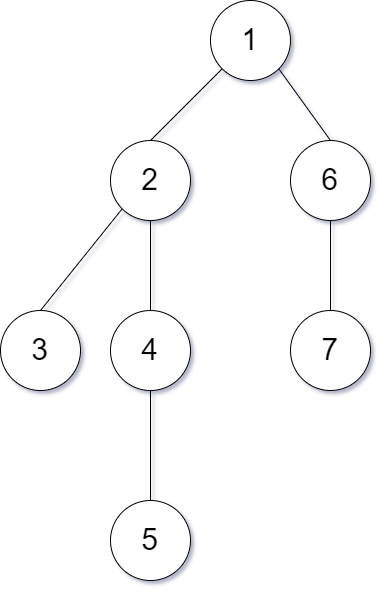
이 트리를 다음과 같이 분리해서
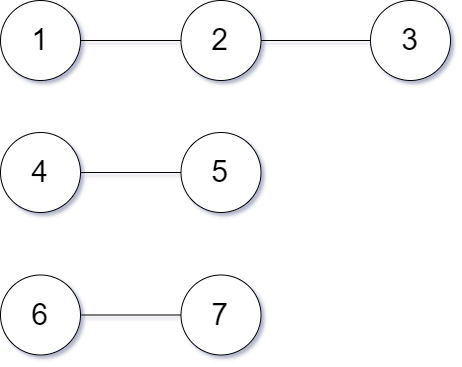
[1,3], [4,5], [6,7] 각 구간 내부는 세그먼트 트리로 관리하고, 구간을 넘나들 때만 따로 처리를 해주면 될 것이다.
[3,7] 경로의 합쿼리를 날린다하면 segQuery(1,3) + segQuery(6,7)과 같은 식으로 답을 구할 수 있다. 이 때의 시간복잡도는 O((경로에서 만나는 구간의 개수)*(각 구간 내에서 쿼리 처리 비용)) 이 될텐데 뒤의 부분은 세그를 쓴다면 logN일테니 앞의 부분을 최대한 줄여야하고, 이 개수를 logN으로 줄이는 방법이 Heavy Light Decomposition이다.
그냥 대충 나누면 logN이 되지않나 생각할 수도 있겠지만
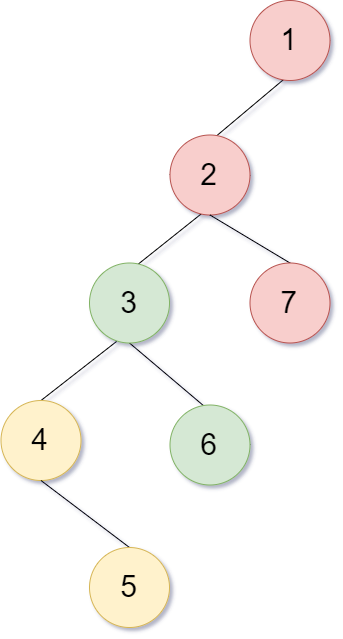
위의 트리에서 같은 색의 정점이 같은 구간으로 나눠졌다고 생각하면 구간의 개수는 N/2에 비례할테니 쿼리 하나를 처리하는데 드는 비용이 O(NlogN)이 될것이다. 위에서 얘기했던 나이브하게 u->v 구간을 하나씩 보는데 드는 비용이 O(N)이었던걸 생각하면 시간과 정성을 들여 시간을 낭비하는 기적의 코드를 만들어낸 것이다.
어떻게해야 "잘" 나눌 수 있을까?
정답부터 말하자면 모든 정점마다 자신을 루트로하는 서브트리의 크기를 계산한 뒤 현재 보고있는 정점부터 자신의 자식 정점 중 가장 크기가 큰 정점으로만 구간을 이어주는 것이다. 이 크기를 정점의 무게라고 한다.
위의 트리를 다시 봐보자.
정점 1의 경우 자식이 하나이므로 2를 이어주고 2의 경우 3은 서브트리의 크기가 4고 7은 1이므로 3을 잇고 7을 다른 구간으로 나눠준다. 같은 방식으로 계속 나눠주면 아래그림과 같이 나눌 수 있는데 어떤 두 정점을 고르더라도 3개를 초과하는 구간을 지날 수 없음을 알 수 있다.
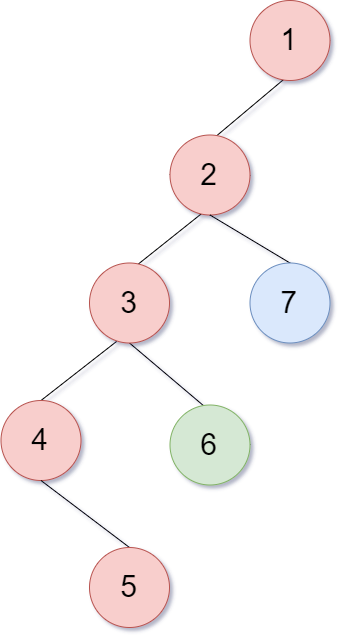
왜 그렇게 될까?
지금 보고있는 정점에서 자식들 중 가장 무거운 정점의 자식을 골라서 구간을 이었다고 하자. 이 때 우리가 봐야할 것은 구간을 잇지 않은 곳에 남아있는 정점들이 최대 몇 개가 될 수 있냐는 것이다. 정점의 개수가 N개라고 하면 서브트리 중 무게가 N/2 이상인 정점이 2개 이상이 될 수 없으므로 무게가 N/2이상인 자식이 있다면 그 자식은 항상 가장 무거운 정점이 되어서 구간이 이어지고, 남은 쪽은 항상 N/2개 미만의 정점만이 남게된다. 따라서 구간이 끊길 때마다 우리가 봐야하는 정점의 개수는 절반 미만으로 항상 줄어들기 때문에 어떤 경로를 선택한다 하더라도 경로 내에서 끊어지는 구간의 개수는 logN 정도임을 알 수 있다.
구현을 해보자
구현부는 dfs 2번을 통해 구간을 나눠주는 부분과 u,v 값을 받아 경로에 대한 쿼리를 처리하는 부분으로 나누어져있다. 먼저 dfs부분부터 살펴보자.
w[u] : u번 정점의 무게
p[u] : u번 정점의 부모의 번호
d[u] : u번 정점의 루트에서부터의 깊이
void dfs(int u)
{
w[u] = 1;
for (auto& v : adj[u])
{
if (!w[v])
{
p[v] = u;
d[v] = d[u] + 1;
dfs(v);
w[u] += w[v];
}
}
}
첫 번째 dfs는 단순히 전체 정점을 순회하면서 무게, 부모, 깊이를 찾는 함수이다. 무게는 2번째 dfs에서 구간을 나누는데 쓰이며, p와 d는 쿼리를 처리할 때 쓰이는 값이다.
cc : 자식들 중 가장 무거운 정점의 번호
n[u] : u번 정점의 넘버링 번호
rev[n[u]] : n[u]번으로 넘버링된 정점의 원래 번호
hld[u] : u번 정점이 속한 구간에서 가장 깊이가 작은 정점의 번호
void dfs2(int u)
{
int cc = -1;
n[u] = ++cnt;
rev[n[u]] = u;
/* 자식들 중 가장 무거운 정점의 번호를 찾음 */
for (auto& v : adj[u])
{
if (p[v] == u && (cc == -1 || w[v] > w[cc]))
cc=v;
}
/* 찾았다면 해당 정점은 현재 정점과 같은 구간으로 만들어주고 먼저 탐색 */
if(cc!=-1) {hld[cc] = hld[u]; dfs2(cc); }
/* 나머지 노드들은 새로운 구간의 첫번째 정점. 이어서 탐색 */
for (auto& v : adj[u])
{
if (p[v] == u && v != cc)
{
hld[v] = v;
dfs2(v);
}
}
}
두 번째 dfs는 첫 번째 dfs에서 알아낸 w값들을 가지고 실제로 구간들을 만들어주는 함수이다.
dfs 넘버링을 할 때 같은 구간에 속해있는 정점들끼리는 연속해야 세그먼트 트리에서 한번에 관리를 할 수 있기 때문에 현재 정점과 구간이 이어지는 정점부터(=자식들 중 가장 무거운 정점부터) 넘버링을 하면서 탐색함에 유의하자. 이렇게 처리를 해주면 새로 넘버링된 번호는 항상 1~N 연속이며, 같은 구간에 있는 정점들은 항상 연속한 번호를 가지기 때문에(반대가 아님을 주의) 세그먼트트리 하나로 전체 값들을 관리할 수 있다. ([1,N] 구간을 가지는 세그먼트트리를 [1,3], [4,8], [9,N] 과 같은 식으로 나눠서 쓴다고 생각하자.)
다음으로 정점에 대한 가중치를 update하는 함수이다.
su(l,r,v) : segment tree update함수
void u(int u, int v, int val)
{
while (hld[u] != hld[v])
{
if (d[hld[u]] < d[hld[v]]) swap(u, v);
su(n[hld[u]], n[u], val);
u = p[hld[u]];
}
if (d[u] > d[v]) swap(u, v);
su(n[u], n[v], val);
}
정점 u,v가 주어졌을 때 두 정점이 같은 구간에 속해있지않다면 둘 중 깊이가 깊은 쪽에서부터 올라온다고 생각하면된다. segment tree에 update를 할 때 [hld[u],u] 가 아니라 [n[hld[u]],n[u]]를 사용함에 주의하자. 또한 해당 정점의 깊이를 비교하는 것이 아니라 hld[u]와 hld[v]의 깊이를 비교해야한다는 것도 주의해야한다. 단순히 u,v깊이를 비교할 경우 아래와 같은 경우에서 [5,7] 구간 쿼리를 할 경우 터질수있다.
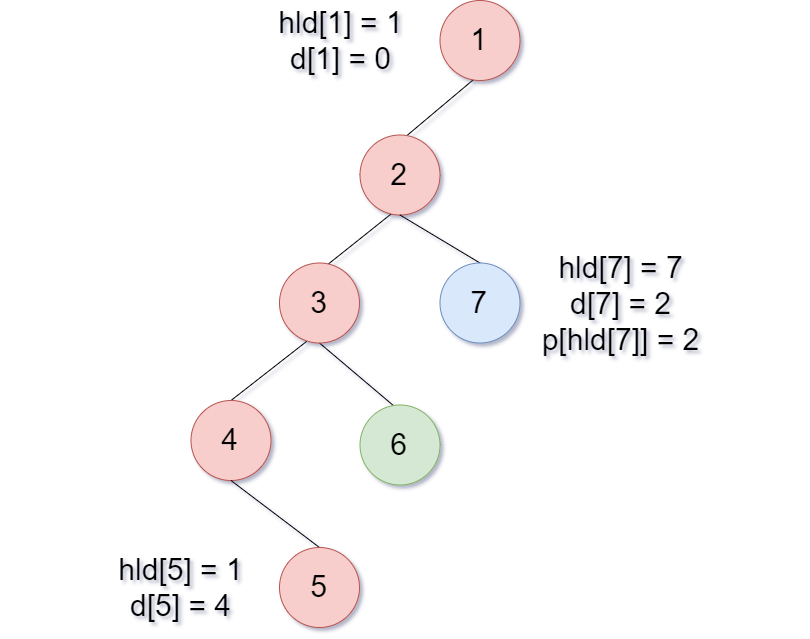
정상적으로 짰다면 u=5, v=7 에서 7을 먼저 처리하고, v=p[hld[7]], 2가되며 2와 5는 같은 구간에 속해있으므로 while문을 빠져나온 뒤, [2,5]를 한번에 처리하게된다.
마지막으로 쿼리함수이다.
sq(l,r) : segment tree query함수
lli q(int u, int v)
{
lli ret = 0;
while (hld[u] != hld[v])
{
if (d[hld[u]] < d[hld[v]]) swap(u, v);
ret += sq(n[hld[u]], n[u]);
u = p[hld[u]];
}
if (d[u] > d[v]) swap(u, v);
return ret + sq(n[u], n[v]);
}
update함수와 동작하는 방식은 같다.
사용하는 변수의 개수도 많고 구현량도 적지않은 편이지만 동작과정이 엄청나게 복잡한 것은 아니기 때문에 함수 흐름을 따라가다보면 이해하는 것 자체는 어렵지 않을것이다. 구현량이 많은거 자체가 싫다면 한두번만 구현해보고 스니펫에 박아둔다음 그때그때 필요한 부분만 고쳐쓰도록하자. 여러분의 손가락은 소중하니까.
추천문제
농장 관리 : https://www.acmicpc.net/problem/5916
트리와 쿼리 1 : https://www.acmicpc.net/problem/13510
트리와 쿼리 3 : https://www.acmicpc.net/problem/13512
남극 탐험 : https://www.acmicpc.net/problem/2927
국제 메시 기구 : https://www.acmicpc.net/problem/17429